Verschiebungen in y-Richtung
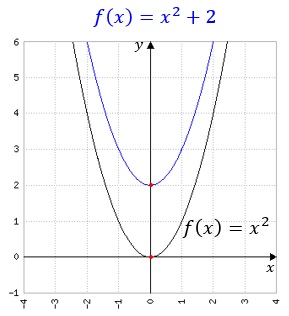
Es sei f(x) eine Funktion, dann stellt f(x)+b eine Verschiebung von f(x) in y-Richtung dar.
Für b>0 handelt es sich um eine Verschiebung um b nach oben, für b<0 ist es eine
Verschiebung um b nach unten.
Verschiebungen in x-Richtung
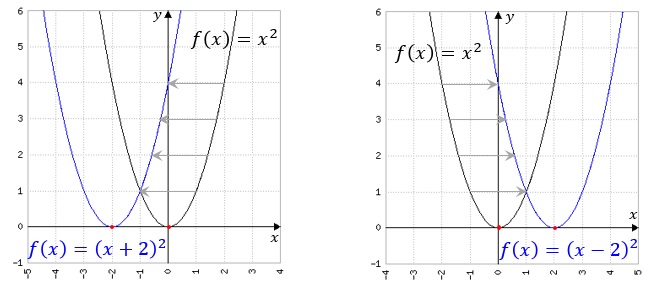
Es sei f(x) eine Funktion, dann stellt f(x+a) eine Verschiebung des Graphen von f(x) in x-Richtung dar. Für a>0 handelt es sich um eine Verschiebung um a Einheiten nach links, für a<0 ist es eine Verschiebung um a Einheiten nach rechts.
Streckungen / Stauchungen
Es sei f(x) eine Funktion, dann stellt c·f(x) eine Streckung in y-Richtung dar, falls c>1 bzw. um eine Stauchung, falls 0<b<1.
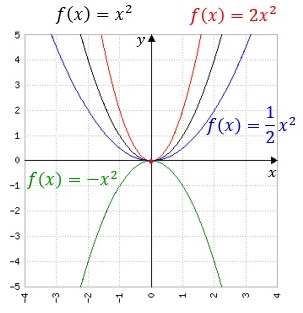
Für c=-1 ergibt sich eine Spiegelung an der x-Achse, was wir später noch einmal ausführlicher erläutern).
Spiegelung an der y-Achse
Es sei f(x) eine Funktion, dann stellt f(-x) die an der y-Achse gespiegelte Funktion dar. Will man eine Funktion an der y-Achse spiegeln, so ersetzt man also im Funktionsterm x einfach durch -x.
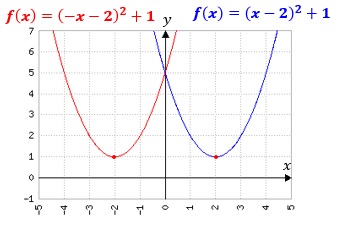
Beispiele:
f(x)=x2 wird zu g(x)=(-x)^2=x2
f(x)=(x-2)3 wird zu g(x)=(-x-2)3
f(x)=sin(-x+1) wird zu g(x)=sin(x+1)
Spiegelung an der x-Achse
Eine Funktion f(x) wird durch Multiplikation mit -1 an der x-Achse gespiegelt. f(x) wird somit zu -f(x).
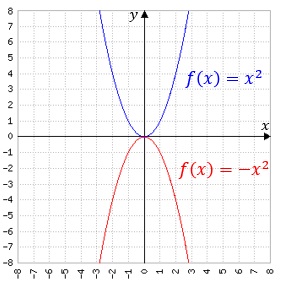
Beispiele:
f(x)=ex wird zu g(x)=-ex
f(x)=x2+2x-1 wird zu g(x)=-x2-2x+1
f(x)=sin(-x+1) wird zu g(x)=-sin(-x+1)
Punktspiegelungen
Eine Punktspiegelung entsteht aus einer Spiegelung an der x-Achse gefolgt von einer Spiegelung an der y-Achse. Aus f(x) wird somit -f(-x).
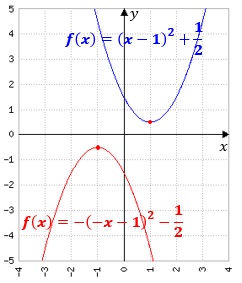
Erkenntnis:
Eine Punktspiegelung ist eine Drehung um 180° am Ursprung.
Beispiele:
f(x)=x2 wird zu g(x)=-(-x)2=-x2
f(x)=(x-2)3 wird zu g(x)=-(-x-2)3=(x+2)3
f(x)=sin(-x+1) wird zu g(x)=-sin(-x+1)
Veranschaulichung mit einigen Excel-Animationen
Schwingungen – Frequenz und Periode
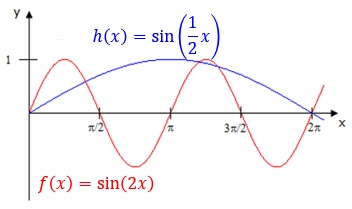
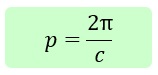
Beispiele:
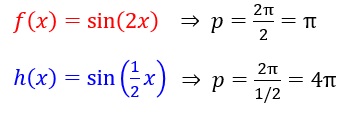
Schwingungen – Streckung / Stauchung / Amplitude
Wie bei allen anderen Funktionen ergibt sich durch Multiplikation mit einem Faktor auch bei Schwingungen eine Streckung oder Stauchung. Damit verändert sich die Amplitude (=Schwingungshöhe).
Beispiele:
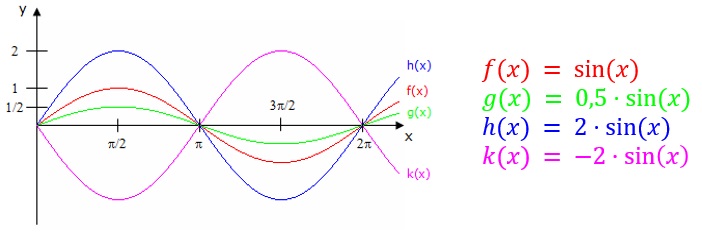
Weitere Eigenschaften
Funktionen haben eine Reihe weiterer Eigenschaften, beispielsweise Nullstellen, Extremstellen, waagrechte und senkrechte Asymptoten usw. Mit diesen Themen beschäftigen wir uns, wenn es um Kurvendiskussion bzw. um Differenzialrechnung geht.
Zusammenfassung
| Allgemeine Funktionen | |
| Verschieben in y-Richtung: | f(x) → f(x)+b |
| Verschieben in x-Richtung: | f(x) → f(x+a) |
| Stauchen/Strecken in y-Richtung: | f(x) → c·f(x) |
| Spiegeln an der x-Achse: | f(x) → -f(x) |
| Spiegeln an der y-Achse: | f(x) → f(-x) |
| Punktspiegelung am Ursprung: | f(x) → -f(-x) |
| Stauchen/Strecken in x-Richtung: | f(x) → f(c·x) |
| Schwingungen | |
| Frequenz ändern: | f(x) → f(c·x) |
| Amplitude ändern: | f(x) → c·f(x) |
| Downloads |
PowerPoint